Ejercicio de análisis. Paeg junio 2013 Castilla la Mancha
- Detalles
- Categoría: 2º Bachillerato
- Publicado el Martes, 17 Diciembre 2013 15:31
- Escrito por Mariano Herrero
Calcula el valor del parámetro a € R, a > 0, para que el valor (en unidades de superficie) del área de la región determinada por la parábola f(x) = – x2 + a2 y el eje de abscisas, coincida con la pendiente de la recta tangente a la gráfica f(x) en el punto de abscisa x = – a Matemáticas II propuesta A Castilla la Mancha junio 2013
El problema está claro: por un lado debemos hallar el área limitada por la parábola con el eje X y por otro el valor de la derivada en x = –a e igualar ambos resultados
Hagamos un esbozo de la función parabólica:
El corte con el eje X: f(x) = – x2 + a2 = 0 nos da los puntos (– a, 0) y (a, 0)
El corte con el eje Y: f(0) = a2 es (0, a2) que coincide con el vértice. La gráfica correspondiente es: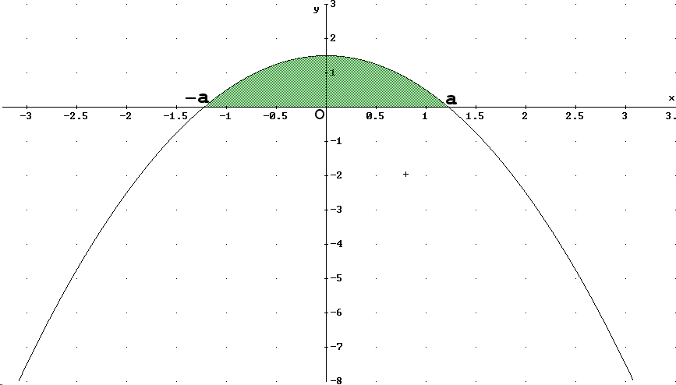
La función es par (la parábola es simétrica respecto del eje Y) y el área pedida es: 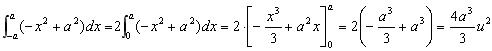
Por otro lado debemos conocer que según la interpretación geométrica de la derivada
“La pendiente m de la recta tangente a una curva en un punto es el valor de la derivada en dicho punto.”
La derivada es f´(x) = – 2x => f´(–a) = – 2(–a) = 2a
Igualando ambos valores: 4a3/3 = 2a => 4a3 = 6a => 4a3 – 6a = 0 => 2a(2a2 –3) = 0
Cuyas soluciones son a = 0
2a2 –3 = 0 (ecuación de segundo grado sin término independiente) => 2a2 = 3 y despejando a = ±![]()
Según enunciado a > 0, luego única solución: a = ![]()


