Sistema dependiente de un parámetro. Paeg Madrid junio 2013

• 
• 

Detalles

Categoría: 2º Bachillerato

Publicado el Sábado, 04 Enero 2014 18:28

Escrito por Mariano Herrero

Dado el sistema de ecuaciones lineales: 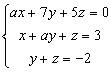   se pide:
a) Discutirlo según los valores de  a.
b) Resolverlo en el caso  a = 4.
c) Resolverlo en el caso  a = 2.                Paeg Madrid junio 2013    Matemáticas II

Tenemos dos métodos interesantes para resolverlo: Uno por determinantes, donde una vez discutido el sistema, debemos por Cramer resolver el sistema dos veces, una para  a = 4 y otra para  a = 2. El otro método es por Gauss, que para éste ejercicio considero más efectivo (el parámetro sólo aparece en dos posiciones), pues a la vez que estudiamos su discusión casi tenemos resueltos los dos sistemas.

a) Para facilitar la tarea se van a intercambiar filas y columnas para que el parámetro  a  no aparezca en la diagonal principal y evitar posibles problemas con el rango.
Nota: Al permutar las columnas 1ª y 3ª, también se permutan la incógnitas  x  con la  z
    x     y    z                              x    y     z                              z     y    x                             z       y        x                                            z      y            x


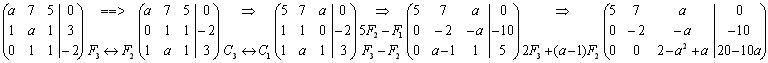
Utilizando Teorema de Rouche-Frobenius y discusión de sistemas por Gauss:
Nos fijamos en el elemento de la matriz de coeficientes  a₃₃ = 2 – a² – a. Resolviendo esta ecuación de segundo grado nos da como soluciones  a = 2 y  a = –1

Por tanto si  a = 2  ó  a = –1  =>  rango(A) = 2
si  a ≠ 2  y  a ≠ –1  =>  rango(A) = 3

Para la matriz ampliada: Nos fijamos en el elemento  a₃₄ = 20 –10a.
Para  a = 2 =>  20 –10a = 0, y el rango es 2
Así pues si  a = 2  =>  rango(A) = rango(A/B) = 2 < nº incógnitas =>  S. C. Indeterminado

Por Gauss nos queda la última fila  0, 0, 0 Ι 0, que podemos suprimir obteniendo un sistema indeterminado de 2 ecuaciones con tres incógnitas.

Para  a = –1  =>  20 –10a = 20 + 10 = 30 ≠ 0  y el rango (A/B) = 3 ≠ rango(A) = 2  =>  Sistema incompatible.
Por Gauss la 3ª fila resulta  0, 0, 0 Ι 30,  que indica una situación absurda  =>  Sistema incompatible

Resumiendo:
- Si  a ≠ 2 y  a ≠ –1 =>  rango(A) = rango (A/B) = 3 = nº incógnitas =>  S. C. Determinado (solución única)
- si  a = 2 =>  rango(A) = rango (A/B) = 2 < nº incógnitas =>  S. C. Indeterminado (infinitas soluciones)
- si  a = –1 =>  rango(A) = 2 ≠ rango (A/B) = 3  =>  Sistema incompatible.

b) Para  a = 4 el sistema obtenido es: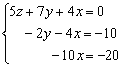

Por el método de sustitución hacia arriba: De la 3ª ecuación: –10x = – 20  => x = 2.
Entrando en la 2ª con  x = 2: –2y – 4·2 = –10  =>  y = 1.
Con los valores de  x = 2  e  y = 1 sustituimos en la 1ª: 5z + 7·1 + 4·2 = 0 => z = 3
Solución para  a = 4: x = 2; y = 1; z = 3

c) Para  a = 2 el sistema equivalente es:

Simplificando la 2ª ecuación queda: y + x = 5 => x = 5 – y. Puesto que el sistema es indeterminado, dependerá de un parámetro  t: haciendo el cambio  y = t  => x = 5 – t.
Sustituyendo los valores de  x  e  y  en la 1ª ecuación: 5z + 7t + 2(5 – t) = 0  => 5z + 7t + 10 – 2t = 0  =>  5z + 5t + 10 = 0  =>  z = –2 – t

Luego solución para  a = 2: x = 5 – t; y = t; z = –2 – t

• Siguiente >